διανεμητικη-δικαιοσυνη

Η ανισότητα είναι μια από τις οικονομολογικές και πολιτικές μόδες της εποχής, πιθανώς ορθά. Μέχρι και εγώ έγραψα σχετικά τα δικά μου.

Αλλά δεν μπορώ να βρω την σωστή κατανομή ρε γαμώτο. Προσπάθησα ωστόσο να κατεβάσω μερικές ιδέες:

Η χρυσή κατανομή.

Η ιδέα της χρυσής κατανομής βασίζεται στην χρυσή τομή. Αν θυμάστε από το σχολείο, η χρυσή τομή, που συμβολίζεται με φ, ισούται με το μισό του αθροίσματος 1 + ρίζα5 και δηλώνει την σχέση δύο αριθμών τέτοιων που να ισχύη ότι α+β/α = α/β. Κατά προσέγγιση δηλαδή 1,618.

Η χρυσή τομή θεωρήθηκε ιστορικά ότι αντιπροσωπεύει το άριστο αισθητικό αποτέλεσμα: ένα ορθογώνιο ούτε πολύ στενόμακρο ούτε πολύ μακρόστενο, αλλά χαραγμένο με μέτρο και αρμονία. Εντάξει, ντε κολόριμπους νον ντισπουτάντουμ μεν, αλλά ας προσπαθήσουμε να εφαρμόσουμε την ιδέα αυτή στην εισοδηματική μας κατανομή, να δούμε τι θα βγη.

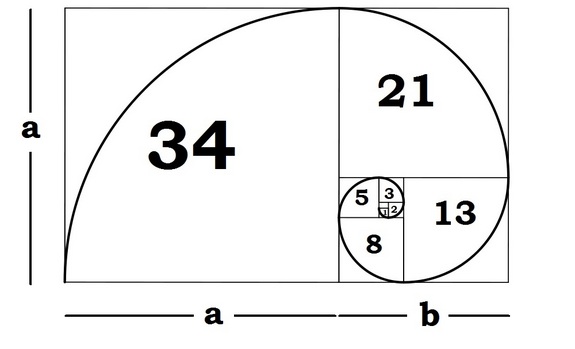
Δεδομένου ότι η διαίρεση δύο συνεχόμενων αριθμών Φιμπονάτσι μεταξύ τους δίνει κατά προσέγγιση την χρυσή τομή φ, βρίσκουμε μια συνεχόμενη δεκάδα φιβονάκειων αριθμών τέτοια που να συναθροίζεται σε 100 περίπου (γιατί εκατό εκατοστά εισοδήματος θέλουμε να κατανείμουμε). Έτσι, παίρνουμε το σύνολο [5, 8, 13, 21, 34, 55, 89, 144, 233, 377], με άθροισμα 979. Τα υπόλοιπα 21 χιλιοστά (979+21=1000) θα τα χαρίσω κατ’ αναλογίαν στα τέσσερα κατώτερα εισοδηματικά κλιμάκια Ζ, Η, Θ, Ι χάριν επιεικείας, αλλά και επειδή όσο πιο μικροί είναι οι φιβονάκειοι αριθμοί, τόσο χειρότερη η προσέγγιση του φ ούτως ή άλλως (άρα το 5 τελικά γίνεται 7, το 8 γίνεται 12, το 13 γίνεται 19 και το 21 γίνεται 30 με στρογγυλοποίηση). Συμπερασματικά λοιπόν, η χρυσή μας ακολουθία είναι η εξής:

7 + 12 + 19 + 30 + 34 + 55 + 89 + 144 + 233 + 377 = 1000 χιλιοστά εισοδήματος. Κάθε αριθμός αντιπροσωπεύει μία εισοδηματική τάξη κατά φθίνουσα σειρά από τα δεξιά προς τα αριστερά, ήτοι Α προς Ι. Υπάρχει μια αρκετά σοβαρή απομάκρυνση από τον χρυσό κανόνα στην μετάβαση ΣΤ/Ζ (34/30 = 1,133), αλλά τέλος πάντων. Πάρα πολύ ωραία.

Read moreΠερί εισοδηματικής ανισότητας ΙΙ: αναζητώντας την χρυσή κατανομή

Έχει προτείνει κανείς συγκεκριμένα ποσοστά εισοδήματος επί του ΑΕΠ ως ιδανικά για το ανώτερο εκατοστημόριο και δεκατημόριο του πληθυσμού;

Θέλω να πω, όλοι (οι κατά πολύ περισσότεροι τέλος πάντων) θρηνούν την ανισότητα, την ξορκίζουν, ανακαλύπτουν χάσματα πλουσίων και φτωχών που συνεχώς διευρύνονται και τα λοιπά και τα λοιπά. Κανείς όμως, εξ όσων γνωρίζω, δεν προτείνει πόση ακριβώς ανισότητα κρίνει δίκαιη για μια κοινωνία, με συγκεκριμένους αριθμούς και όχι με το μίγμα κλάψας και κατάρας στο οποίο είμαστε συνηθισμένοι.

Προσπάθησα λοιπόν εγώ, με τις ασθενείς μου δυνάμεις, να βάλω μια τάξη στο ζήτημα. Αν κάποιος γνωρίζη σχετικά περισσότερα και μπορή να υποδείξη και κανένα προσβάσιμο σύνδεσμο, να μην σιωπήση!

Κατατάσσουμε λοιπόν τον πληθυσμό σε δέκα εισοδηματικές τάξεις, στις οποίες αντιστοιχούμε δέκα ποσοστά εθνικού εισοδήματος, ονομάζοντάς τις από την ανώτερη προς την κατώτερη με Α έως Ι. Κάθε ανώτερο δεκατημόριο πληθυσμού απολαμβάνει υποχρεωτικά μεγαλύτερο ποσοστό εισοδήματος από το αμέσως κατώτερό του (Α>Β>Γ>Δ κ.ο.κ.). Μάλιστα, υπάρχει μια ιδιόμορφη συμμετρικότητα μεταξύ των τάξεων, καθώς κάθε εκατοστημόριο εισοδήματος που προικίζει το ανώτερο, πρώτο 10%, δηλ. το Α, αφαιρείται από το κατώτερο, δέκατο 10%, δηλ. το Ι (και όχι από το Θ ας πούμε) κ.ο.κ. Αντιστοιχούμε συνεπώς κάθε δέκατο πληθυσμού με συγκεκριμένο ποσοστό εισοδήματος, ώστε να εξαντλήται το διαθέσιμο εισόδημα. Χάριν ευκολίας, χρησιμοποιώ μόνο ακέραιους, με μικρότερη την μονάδα.

Και ας πάρουμε τώρα περιπτώσεις:

1. Εξισωτισμός.

Όπου το κάθε δεκατημόριο πληθυσμού αντιστοιχεί σε ακριβώς ένα δέκατο του εθνικού εισοδήματος. Όπου, με άλλα λόγια, δεν έχει νόημα καμία διάκριση του πληθυσμού βάσει εισοδήματος, αφού σε όλους προσνέμεται ίσο κατά κεφαλήν εισόδημα.

Αυτή η στατιστικά απίθανη περίπτωση δεν νομίζω ότι εκπροσωπείται πολιτικά. Δηλαδή, όχι μόνο στον πραγματικό κόσμο δεν έχει παρατηρηθή ποτέ κοινωνία όπου απολαμβάνουν το ίδιο εισόδημα το νήπιο με τον ενήλικα και ο εργατικός με τον οκνηρό, αλλά και στην πολιτική θεωρία δεν νομίζω ότι υπάρχει κάποιος που το έχει υποστηρίξει. Στο κάτω κάτω, ακόμα και οι κομμουνιστές δογματίζουν “jedem nach seinen Bedürfnissen!”.

Το ενδιαφέρον σημείο του άκρου εξισωτισμού που θα ήθελα εγώ να τονίσω είναι άλλο: είναι άδικος. Όχι μόνο δεν μπορεί να υπάρξη, αλλά δεν πρέπει κιόλας. Ένα ποσό ανισότητας είναι απαραίτητο ήδη για λόγους δικαιοσύνης, απλώς και μόνο επειδή ως μοναδικές και ανεπανάληπτες προσωπικότητες διαφέρουμε καθ’ όλους τους κρίσιμους παράγοντες: εργατικότητα, παραγωγικότητα, επινοητικότητα, εκπαίδευση, ηλικία, ρώμη, ευφυΐα, ακόμη και τύχη.

Read moreΠερί εισοδηματικής ανισότητας

Στο γύρισμα του προηγούμενου αιώνα ο Ιούλιος Βερν έγραψε ένα ακόμη μυθιστόρημά του: La Chasse au météore.

Στο βιβλίο αυτό δύο ερασιτέχνες αστρονόμοι ανακαλύπτουν ένα καινούργιο μετεωρίτη να πλησιάζη την Γη. Αποκαλύπτεται μάλιστα ότι ο μετεωρίτης είναι ολόχρυσος. Η φαντασία των πτωχών Γήινων εξάπτεται, όταν μάλιστα ένας ημίτρελος επιστήμονας με το αξιομνημόνευτο όνομα Ζεφυρίνος Ξιρδάλης επιτυγχάνει να εξαναγκάση τον αερόλιθο σε αναγκαστική προσγείωση. 5 με 6 δισεκατομμύρια φράγκα σε καθαρό χρυσό.

Οπότε, το προφανές ερώτημα είναι: σε ποιον ανήκει ο χρυσός;

Read moreΗ διανεμητική δικαιοσύνη παρ’ Ιουλίω Βερν

Ιστολογική πενία τέχνας κατεργάζεται. Εν προκειμένω, άμα δεν υπάρχει έμπνευση, καλή είναι και η αντιγραφή.

Μεταφράζω λοιπόν και διασκευάζω εν τω άμα μια σελίδα από το Anarchy, State and Utopia του Nozick, σελ. 160-161:

Ας υποθέσουμε ότι πραγματοποιείται μια κατανομή που ευνοείται από κάποια από τις θεωρίες περί δικαιοσύνης που δεν στηρίζονται στις αξιώσεις. Ας υποθέσουμε ότι είναι η αγαπημένη σας κατανομή, ας την ονομάσουμε δε κατανομή Κ1. Σε αυτήν, μπορεί όλοι να έχουν ίσο μερίδιο, μπορεί όμως και τα μερίδια να κυμαίνωνται σύμφωνα με κάποια μεταβλητή που εκτιμάτε πολύ. Τώρα ας υποθέσουμε ότι ο Βίλτων Σαμβερλαίνος Βασιλεύς ΛεΒρόνος έχει μεγάλη ζήτηση στις ομάδες μπάσκετ, καθώς είναι μεγάλος κράχτης (ας υποθέσουμε επίσης ότι τα συμβόλαια είναι μονοετή και ότι οι παίκτες μετά γίνονται ελεύθεροι). Υπογράφει λοιπόν με κάποια ομάδα το ακόλουθο συμβόλαιο: για κάθε εντός έδρας παιχνίδι εισπράττει 1 ευρώ από την τιμή κάθε εισιτηρίου (αγνοούμε στο μεταξύ το ερώτημα αν η συμφωνία αυτή γδύνει τους ιδιοκτήτες της ομάδας, αφήνοντάς τους να ρυθμίσουν μόνοι τους τα του οίκου τους). Το λοιπόν, η αγωνιστική περίοδος αρχίζει και ο φίλαθλος κόσμος πηγαίνει στο γήπεδο για τους αγώνες της ομάδας του κατενθουσιασμένος. Όλοι αγοράζουν τα εισιτήριά τους, βάζοντας κάθε φορά 1 ευρώ από την τιμή εισόδου χωριστά σε ένα ειδικό κουτί στο όνομα του ΛεΒρόνου. Ενθουσιάζονται βλέποντάς τον να παίζη, γιατί για αυτούς αξίζει όλα τα λεφτά του εισιτηρίου.

Read moreΜικρό περί διανεμητικής δικαιοσύνης

Είχε έρθει λοιπόν ήδη ο κακός χειμώνας. Το μυρμηγκάκι καθόταν μπροστά στο ζεστό τζάκι του, όπου έκαιγε ένα χοντρό κούτσουρο. Στην φωτιά έβραζε ένα τσουκάλι τραχανάς. Το μυρμηγκάκι έβγαλε τις παντόφλες του, άπλωσε τα ποδαράκια του και άνοιξε την Καθημερινή. Να δούμε και τι γίνεται στον έξω κόσμο.

Ξαφνικά, και ενώ έξω λυσσομανούσε η θύελλα και ο παγωμένος βοριάς φυσούσε, το μυρμηγκάκι άκουσε στην πόρτα ένα κλοπ-κλοπ-κλοπ. Μπα, ποιος να είναι τέτοια ώρα. Λες να είναι κανάς συνδικαλιστής της ΔΕΗ; Λες να είναι κανένας ανεύθυνος λαϊκιστής;

Ξανά κλοπ-κλοπ-κλοπ.

Read moreΜύρμηξ και τέττιξ 2.0