Μπαίνω σε ξένα χωράφια τώρα και μπορεί να γράψω και βλακείες, σχωράτε.
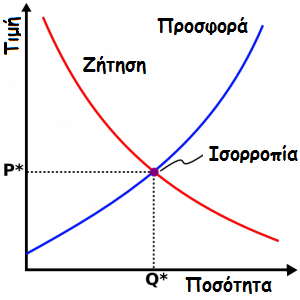
Στην Μικροοικονομία μιλάμε για το σημείο ισορροπίας μιας ανταγωνιστικής αγοράς, για το σημείο δηλαδή όπου τέμνονται οι καμπύλες γραμμές της προσφοράς και της ζήτησης. Κάπως έτσι δηλαδή:
Στο σχήμα αυτό βλέπουμε ότι όλα είναι πολύ κομψά: η αγορά ισορροπεί σε ένα και μοναδικό γεωμετρικό σημείο και μάλιστα προσφορά και ζήτηση δεν θα μπορούσαν να συναντηθούν πουθενά αλλού. Αλλά η πραγματικότητα, όπως γνωρίζουμε, είναι πιο περίπλοκη.
Η βασική ιδέα μου είναι ότι είναι λάθος να μιλάμε για καμπύλες προσφοράς και ζήτησης, γιατί πρόκειται για μια κακή μεταφορά. Στην πραγματικότητα δεν έχουμε να κάνουμε με γραμμές, ήτοι για μια αλληλοδιαδοχή μονοδιάστατων σημείων, αλλά με ταινίες καμπύλης και ζήτησης, ταινίες που έχουν σαφές πλάτος.
Πράγματι, τόσο ο πωλητής όσο και ο αγοραστής δεν εστιάζουν σε μία και μοναδική στατική τιμή, οποιαδήποτε απόκλιση από την οποία οδηγεί σε απόσυρση του ενδιαφέροντός τους και, άρα, σε ματαίωση της συναλλαγής. Δεν υπάρχει δηλαδή μια μοναδική τιμή με πιθανότητα συναλλαγής 100% και άπειρες τιμές με πιθανότητα ίση με το μηδέν, όπως υπονοεί η συνήθης γραφική απεικόνιση. Κανείς δεν αποφασίζει ότι η τιμή του είναι π.χ. 100 ευρώ, πολύ περισσότερο δε 100,3 ευρώ ή 100,37 ευρώ ή 100,378 ευρώ. Αλλά στην πραγματικότητα, όπως όλοι μας γνωρίζουμε, αποδέχεται ένα εύλογο εύρος τιμών, π.χ. 96 (αν πωλεί) με 104 (αν αγοράζει) ευρώ, εντός του οποίου διατίθεται να συμβληθή. Πρέπει να παρατηρήσουμε επίσης ότι εντός του εύρους αυτού δεν είναι όλα τα σημεία αυτής ταινίας ισοπίθανα, αλλά η μετάβαση από την μία τιμή στην άλλη είναι σταδιακή και όχι ψηφιακή: ο πωλητής πωλεί με πιθανότητα 100% στα 100 ευρώ και πιο πάνω, αλλά ίσως μόνο με πιθανότητα 20% στην κατώτατη τιμή του των 96 ευρώ. Αυτό δεν σημαίνει όμως ότι η είναι αδύνατη η συναλλαγή στα 96 ευρώ, ήτοι ότι η αγορά δεν ισορροπεί (με μικρότερη πιθανότητα ασφαλώς) και εκεί.
Εκείνο που παραλλάσσει λοιπόν είναι η πιθανότητα με την οποία θα συνήπτε την σύμβαση στην τιμή που αποκλίνει από την ιδεώδη του ο κάθε συμβαλλόμενος. Στο παράδειγμά μας, ο πωλητής θα συμφωνούσε ενδεχομένως με πιθανότητα 20% στα 96 ευρώ, 40% στα 97 ευρώ κ.ο.κ. έως 100% στα 100 ευρώ. Αντίστροφα, ο αγοραστής θα συμφωνούσε με 20% στα 104 ευρώ, 40% στα 103 ευρώ κ.ο.κ. έως 100% στα 100 ευρώ. Γραφηματικά αυτό αναπαρίσταται με αποχρώσεις του ίδιου χρώματος, που σταδιακά σκουραίνει σε κάθε τιμή, μέχρι την τιμή της κατεξοχήν ισορροπίας.
[Κατ’ ακρίβειαν βέβαια, το εύρος τιμών που καλύπτουν οι ταινίες προσφοράς και ζήτησης είναι πολύ εκτενέστερο, αν αναλογιστούμε ότι υπό συνθήκες ανάγκης (π.χ. ταμειακής ασφυξίας) μια επιχείρηση ίσως πωλήση και κάτω του κόστους ακόμη, ενώ, αντίστοιχα, και ο αγοραστής ίσως είναι διατεθειμένος να καταβάλη ένα υπέρογκο ποσό (αν π.χ. το αντικείμενο της πώλησης έχει για αυτόν συναισθηματική αξία). Για πρακτικούς λόγους όμως, αρκεί να περιοριστούμε σε μεγαλύτερες πιθανότητες].
Κατ’ αυτόν τον τρόπο λοιπόν, κάθε τιμή μετέχει περισσοτέρων ταινιών προσφοράς και ζήτησης, στην καθεμία με διαφορετικά ποσοστά. Από κοινού τώρα οι ταινίες προσφοράς και ζήτησης τεμνόμενες δεν παράγουν, κατά συνέπεια, ένα ευκλείδειο σημείο, αλλά ένα πλάγιο παραλληλόγραμμο. Εντός αυτού, το καθαυτό σημείο ισορροπίας ορίζεται στην τομή των διαγωνίων του (μπορεί να είναι και τετράγωνο ισορροπίας στην περίπτωση που οι ταινίες προσφοράς και ζήτησης είναι ταυτοπλατείς).
Δεν ξέρω αν βοηθούν κανένα όλα αυτά, αλλά τα σκεφτόμουνα και είπα να τα γράψω. :-)
Ωραίοι οι προβληματισμοί σου Αθανάσιε. Οι καμπύλες προσφοράς όπως παρουσιάζονται σε εισαγωγικά εγχειρίδια οικονομικών δεν αποτελούν τίποτα περισσότερο από εξαιρετικά απλά και ακατέργαστα εργαλεία. Είναι σαν να προσπαθούμε να αναλύσουμε τις μορφές που παρατηρούμε στο φυσικό κόσμο χρησιμοποιώντας ως εργαλεία μόνο ευθείες γραμμές και λείες καμπύλες. Μια χονδρική αναπαράσταση -τη σίγουρα ευκολότερα αντιληπτή στο ευρύ κοινό- ίσως να μπορέσουμε να επιτύχουμε αλλά σίγουρα θα αποτύχουμε να περιγράψουμε τη περιπλοκότητα του φυσικού μας κόσμου και ίσως συχνά να οδηγηθούμε σε λάθος περιγραφές/συμπεράσματα.
Ωστόσο οι ειδικοί που ασχολούνται με τις ανθρώπινες επιλογές δεν χρησιμοποιούν τις γραμμές προκειμένου να αναλύσουν τις ανθρώπινες καταναλωτικές συμπεριφορές υποθέτωντας ταυτόχρονα τον ντετερμινισμό των απλούστερων αναλυτικών εργαλείων. Η αυτονόητη αποδοχή τους είναι πως επιλογή είναι στοχαστική, ετερογενής και επηρεάζεται από μια σειρά παρατηρούμενων και μη παραγόντων. Δεν επιχειρούμε να εκτιμήσουμε λοιπόν ντετερμινιστικές ποσότητες αλλά πιθανότητες ή κατανομές πιθανοτήτων (αν ενδιαφέρεσαι ρίξε μια ματιά σε discrete choice models, probit, logit κοκ). Ομολογώ λοιπών πως η διαίσθηση σε οδήγησε στο σωστό συμπέρασμα. O τρόπος βέβαια με τον οποίο μπορεί να έρθει η ισορροπία μπορεί να είναι πολύπλοκος (διαφορετικά εργαλεία προτείνονται με διαφορετική επιτυχία ανάλογα με την αγορά την οποία επιχειρούν να μοντελοποιήσουν) ή η ισορροπία μπορεί να μη προκύπτει καν.
Ξαναλέω πάντως πως βρίσκω πολύ εύστοχο τον προβληματισμό σου αφού αναγνωρίζω πως η βολική υπόθεση του ντετερμινισμού έχει επηρεάσει σημαντικά το τρόπο σκέψης των οικονομολόγων και για αυτό και ορισμένες προσεγγίσεις τους είναι σε μεγάλο βαθμό μη ικανοποιητικές ή και στρεβλές.
θα προσθεσω καταρχας οτι οι καμπυλες ζητησης και προσφορας, οταν γινονται σωστα, δεν ειναι υποθεσεις-παραδοχες-πωςτιςλενε (assumptions), αλλα αποτελεσματα πολυ βαθυτερων υποθεσεων.
Η καμπυλη ζητησης βασικα βγαινει απο το maximum willingess to pay, που για ενα γνωστο πρϊον ειναι σιγουρα ενα συγκεκριμενο σημειο, αλλα και για αγνωστο προϊον είναι απλα expectation, αρα παλι ενα σημειο.
OK Σωτηρη, αλλα ποσο μετρησιμη εναι αυτη η Θεληση Προς Πληρωμη εμπειρικα? Στις πειραματικες μετρησεις οι ΘΠΠ εχουν βρεθει να εξαρτωνται απο ασημαντες λεπτομερεις του περιβαλλοντος. Και δεν θα επρεπε αντιθετα η ιδια η ΘΠΠ να εχει σαν βαση την ‘εκτιμηση των μελλοντικων ηδονων’ απο την καταναλωση του αγαθου?
http://users.nber.org/~rosenbla/econ311-05/syllabus/stabledemand.pdf
Οι ALP βρισκουν οτι οι μετρωμενες ΘΠΠ ειναι απιστευτα αυθαιρετες, ακομη και για κοινα και απλα αγαθα.
Εμεις βεβαια δεν πιστευουμε οτι το μεγεθος αυτων των μετρτησεων γενικευεται, αλλα και παλι το θεμα δεν ειναι τοσο απλο επηστημολογικα οσο θα θελαμε, ε Σωτηρη? Τι σημαινει ακριβως ‘ειναι ενα σημειο’ οταν αυτο το σημειο ειναι αρκετα (η εστω καπως) αυθαιρετο?
Οι καμπυλές ναι είναι μια απλοποίηση του κόσμου αφού δεν απεικονίζουν ούτε τον τυχαίο και χρονομεταβλητό τρόπο με τον οποίο κάνουμε τις επιλογές μας, ούτε τους μηχανισμούς μέσω των οποίων γίνεται το matching μεταξύ των αντίθετων πλευρών. Μια διασταύρωση μεταξύ δύο γραμμών ισοδυναμεί με την ακαριαία ισορροπία. Γνωρίζουμε πως οι επιλογές μας είναι τυχαίες και αυτό είναι συνεπακόλουθο της ελεύθερης μας βούλησης. Συχνά οι επιλογές μας δεν είναι αποτέλεσμα των προτιμήσεων μας αλλά γίνονται χωρίς αυτές καν να υπάρχουν (δες το άρθρο “Choice without preference” του φιλόσοφου Rescher και το ωραίο του βιβλίο “Luck” -ειδικά κεφ 2). Δεν υπάρχουν αιτιώδεις κανόνες που να προσδιορίζουν πλήρως τη συμπεριφορά μας. Συνεπώς η συμπεριφορά μας αποτελεί μερικώς συνάρτηση τυχαίων και πιθανότατα αλλοπρόσαλλα συμπεριφερόμενων μεταβλητών. Συνεπώς η WTP ως συνάρτηση τυχαίων μεταβλητών δεν αποτελεί κάποιο σταθερό σημείο αλλά είναι εξ ορισμού μια τυχαία μεταβλητή (ή καλύτερα μια στοχαστική διαδικασία). Αυτό που προσπαθούμε να παρατηρήσουμε (και είναι δύσκολο όπως σωστά ο Ζαχαρίας επισημαίνει) δεν είναι συνεπώς την ίδια τη τυχαία μεταβλητή (ή στοχαστική διαδικασία) WTP αλλά κάποιο realization αυτής. Και μέσω αυτού του realization προσπαθούμε να εκτιμήσουμε τις ιδιότητες της τυχαίας μεταβλητής – δηλαδή τα χαρακτηριστικά που περιγράφουν την κατανομή της. Τώρα και στις περιπτώσεις του γνωστού προϊόντος και στη περίπτωση του άγνωστου ναι μεν μπορεί μέρος του output μας να είναι κάποιοι point estimates αλλά δεν πρέπει να ξεχνάμε πως οι point estimates έχουν συγκεκριμένες ιδιότητες. Όπως στατιστική κατανομή που προσδιορίζει τα διαστήματα εμπιστοσύνης ( που είναι κατά κάποιο τρόπο οι λωρίδες για τις οποίες διαισθητικά μίλησε ο ΑΑ) τους και μας επιτρέπει να κάνουμε ελέγχους υποθέσεων. Δύο point estimates με την ίδια τιμή δεν έχουν το ίδιο πληροφοριακό περιεχόμενο!
Οι καμπυλες αυτες περιγραφουν δυναμικα συστηματα και γι αυτο καλυτερο εργαλειο για την κατανοηση τους ισως ειναι η θεωρια του Χαους.
Η τιμη ισοροπιας μπορει να θεωρηθει αυτο που στην θεωρια αποκαλειται “παραξενος ελκυστης” γιατι ειναι το σημειο που “ελκυει” ολες τις θεσεις που μπορει να παρει το σημειο ισορροπιας. Με λιγα λογια το σημειο ισορροπιας ειναι το σημειο απο το οποιο δεν απομακρυνονται οι τιμες ισορροπιας ακομη και μετα απο ισχυρες αναταραξεις του συστηματος.
Το σημειο ισορροπιας οπως σωστα επισημαινεται δεν ειναι σταθερο, αλλα εξαρταται απο πολλους παραγοντες περα απο την προσφορα και την ζητηση, οπως καρτελ, κερδοσκοπικα παιχνιδια, πολιτικες παρεμβασεις κ.α
Η αλλαγη ομως πιθανοτατα δεν θα ειναι γραμμικη, αλλα χαοτικη και ανεξελεγκτη. Κατα το γνωστο παραδειγμα τις πεταλουδας που κτυπαει τα φτερα της στο Πεκινο και η αλλαγη μπορει να προκαλεσει καταιγιδα στο Παρισι, μικρες παρεμβασεις στους παραγοντες της αγορας μπορει να προκαλουν μεγαλες μεταβολες στα αποτελεσματα. Η και το αντιστροφο, αφου ο “ελκυστης” του συστηματος φροντιζει το συστημα να κινειται μεσα σε καποια ορια.
Οπως στο παραδειγμα της πεταλουδας, το φτερουγισμα της μπορει να σβησει η να ενισχυθει αναλογως των συνθηκων, αλλα δεν μπορει να φερει αποτελεσματα που κινουνται εξω απο τα ορια που θετουν οι ελκυστες του γηινου κλιματος.
Αυτο εξηγει κατα καποιο τροπο και την εμμονη των φιλελευθερων στην χωρις παρεμβασεις αγορα, αφου καθε παρεμβαση εχει στην πραγματικοτητα ανεξελεγκτα αποτελεσματα και καθιστα αναγκαια μια ακομη για να διορθωθει το αποτελεσμα της πρωτης.
Ισως υπαρχει καποια λογικη σ αυτο. Ισως τελικα αν περιορισεις τις παρεμβασεις στο ελαχιστο δυνατο, να δεις το συστημα να ισορροπει καλυτερα.
Το θεμα ειναι αν θελουμε να ισορροπει σ αυτο το σημειο αλλα και το οτι αυτο δεν μπορει να επιδιωκεται σημερα που οι παρεμβασεις απο την συμμαχια κυβερνησεων και τραπεζων στην οικονομια ειναι καθημερινη πρακτικη.
Ελευθερη αγορα οπου οι τραπεζες κοβουν χαρτακια χωρις αντικρυσμα και τα πουλαν για πλουτο και τα κρατη κανουν συνεδρια και συμφωνιες για επεμβασεις σε επιτοκια, δημοσιες δαπανες, αγοραπωλησιες ομολογων και αλλα τετοια ειναι για γελια.
Θανάση,
χωρίς να μπως στις λεπτομέρειες της ανάρτησης, θα πω ιστορικά κάποια πράγματα.
Όπως σωστά επισημάνανε και άλλοι, το μοντέλο της προσφοράς και της ζήτησης είναι μια απλοποίηση της πραγματικότητας. Ο Λεον Βαλρας εισήγαγε την ιδέα της αγοράς ως δημοπρασία όπου ο δημοπρατητής φωνάζει συνέχεια τιμές ώσπου να βρεθεί η τιμή που εξισώνει τις ποσότητες προσφοράς και ζήτησης και κατόπιν επιτρέπει στους αγοραστές και τους πωλητές να συνδιαλλαγούν σε αυτήν την τιμή μόνο. Όταν ερωτήθηκε, πώς θα συμβεί αυτό στην πραγματικότητα όπου δεν υπάρχει δημοπρατητής αλλά οι συναλλαγές είναι αποκεντρωμένες, απάντησε ότι θα λειτουργήσει μέσω μιας διαδικασιάς δοκιμής και λάθους. Μέχρι το 1955 ωστόσο δεν υπήρχε εμπειρική επαλήθευση. Αυτό συνέβη χάρη στον Vernon Smith ο οποίος πήρε το Νόμπελ για αυτή του τη συνεισφορά. Ο Σμιθ ξεκίνησε να αναθέτει ρόλους αγοραστή και πωλητή στους φοιτητές τους. Κάθε αγοραστής είχε μια ανώτατη τιμή που ήταν διατεθειμένος να πληρώσει και κάποιος πωλητής μια ελάχιστη τιμή που ήταν διατεθειμένος να δεχτεί. Μετά, άφησε τους φοιτητές του να συνδιαλλαγούν σε διαδοχικούς γύρους. Αυτό που παρατήρησε είναι ότι πράγματι, μετά απο μερικούς γύρους, όλοι άρχισαν να συναλλάσσονται στην ίδια τιμή, η οποία επιπλέον ήταν η τιμή ισορροπίας, όπως ο Βαλράς είχε προβλέψει. Παρεπιπτόντως, το ίδιο πείραμα κάνω στην τάξη με τους φοιτητές μου κάθε εξάμηνο, μέσω υπολογιστών (οι συναλλαγές είναι ηλεκτρονικές).
Εδώ βέβαια χρειάζεται μια επισήμανση. Η διαδικασία λειτουργεί ομαλά όταν το προϊον είναι ομοιογενές και είναι εύκολο τόσο στους αγοραστές όσο και στους πωλητές να βρουν πόσο πληρώνουν οι άλλοι για το ίδιο προϊόν. Σε κάποιες αγορές αυτό δεν ισχύει. Παράδειγμα είναι η κτηματομεσιτική αγορά (κάθε σπίτι είναι διαφορετικό από το άλλο) ή η αγορά εργασίας (κάθε εργαζόμενος ή θέση εργασίας είναι διαφορετική από την άλλη). Εκεί, ποιό ρεαλιστικά μοντέλα είναι αυτά που βασίζονται στη λεγόμενη matching theory, τα οποία όμως είναι πιο πολύπλοκα. Σκοπός ενός μοντέλου δεν είναι να είναι ρεαλιστικό, αλλά να είναι χρήσιμο και όσο πιο απλό χρειάζεται αλλά όχι απλούστερο από αυτό. Σε πολλές περιπτώσεις, ακόμα και για την αγορά εργασίας το μοντέλο της προσφοράς και ζήτησης αρκεί για να βοηθήσει στην κατανόηση πολλών φαινομένων.